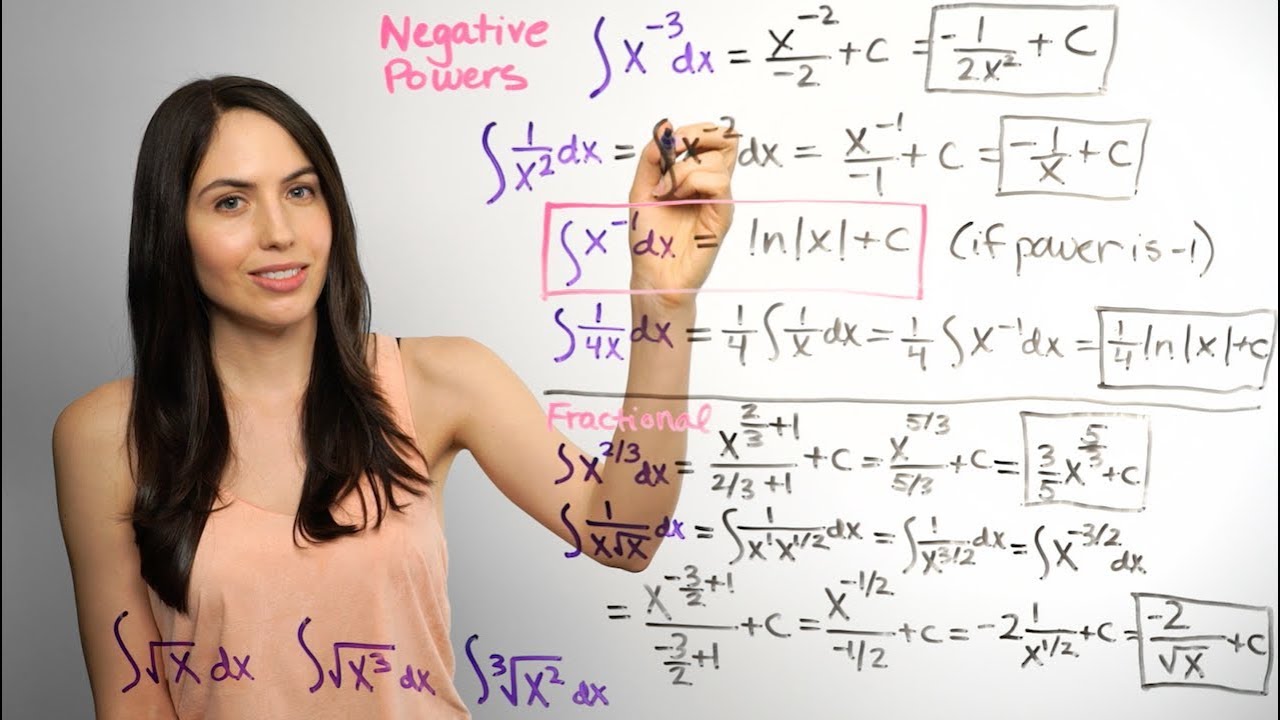CalcAB – edMe Learning

Keep working hard for Friday’s quiz! It will have questions on both the big ideas: calculating areas (integrals) and finding rates of change (derivatives) with a mix of natural logs, exponential functions and u-substitution.

Using Fundamental Theorem of Calculus & U-substitution with Integrals

Using the Power Rule Backwards

This video is the foundational piece for using the power rule backwards to solve integrals. You can use the power rule like normal to check your answers.

Review: Overview of Derivative and Anti-Derivative

Integral of one Term

Solving e^u

Trig Function Integrals

Review: Finding Integrals with Anti-Derivative

Previous Videos

Big picture explanation

This video is good at explaining these ideas conceptually.

Derivatives of Natural Logs

Derivatives of Log Properties

Derivatives of e^x

Derivatives of ln, logs, and e^x

Derivatives of Units 5 & 6 in One Summary

Proofs of ln and e^x Derivatives

Review of Limits: If finding limits seems challenging, you can always review this video.

Heart of Calculus: Applications of Derivatives & Integrals

Mean Value Theorem (formal definition):

Contrasting Average Value and Average Rate of Change

Watch by Sunday:

Mean Value Theorem (informal definition):

Implicit Differentiation is the key to understanding Related Rates problems. Please review both these videos and write down questions with timestamps (like, 8:02) that we can review Sunday.

Optimization Practice

If you can’t solve these questions, then please review the four videos below.

An airplane is flying in a horizontal, straight-line path. The speed of the airplane is 100 meters per second, and its altitude is 1000 meters. What is the rate of change of the angle of elevation, , when the horizontal distance from a reference point P on the ground is 2,000 meter?
A ball is expanding at a rate of 0.25 inches per minute. How is the volume changing?
A cylinder is increasing its height at 2 centimeters per minute. How is its volume changing?

New Overview

Previous Overview: There are five practice worksheets ready now: Limits, Power Rule, Product Rule, Quotient Rule, and Chain Rule. After you finish each sheet, you can click these links after you work through the worksheets for Limits Worksheet Answers, Power Rule Answers, Product Rule Answers, Quotient Rule Answers, and the Chain Rule Answers.

Tuesday we will talk though this limit definition of the derivative one more time. We are going to highlight examples of f(x) and how the structure shows that we are finding f‘(x) at a certain point. I want to talk about the concept so the fluency makes more sense.

$\lim_{h \to 0} \frac{f(x + c) - f(c)}{h}$

You are seeing this definition where f(c) is already solved, so f(c) equals a number like, 1000. Then, we see the structure of the function because f(x + c) is never solved. It just shows how f(x) works. Here are the solution steps we will dive deeply into.

The remainder of this page has definitions and tools that we will review up until the test on Thursday.

Tools/Definitions from the Last Quiz

Definition of a continuous function.

Functions have limits if the left and right limits go to the same place

$\lim_{x \to 1-} f(x) = \lim_{x \to 1+} f(x)$

limit of a piece-wise function

When you have time for a 10-minute video. Here is another voice (Sal Khan!) to help make the piece-wise/continuity/approaching ideas make more sense.

The limit is critical in calculus because it gives us access to the idea of how we can find the rate of change at one point. For most of the next month you will find the rate of change of a graph at one point. You will think about the rate of change as a tangent line to the graph and you will use this limit definition. Be sure to actively take notes during this video to think about how you can identify the function and point where you are finding the rate of change.

Power Rule: The rule we use all the time when we have polynomials (but not rational functions). Here is the simplest example:

$f(x) = x^2, then f'(x) = 2x$

Product rule: This may require some memorization, but what is the derivative of (f(x))(g(x))?

$h(x) = (3x-7)x^2, then h'(x) = (3)(x^2)+(3x-7)(2x)$

We say something like “Derivative of the first times the second plus the derivative of second times the first.”

Because we now have the quotient rule, I am going to encourage us to keep this idea of derivative of one times the other. The product rule has the sum of these two types. The quotient rule has the difference of these two types (and a denominator).

Quotient Rule: For rationale functions we can’t use the Power Rule and the Chain Rule is too complicated. We use this rule for functions like:

$\frac{(5x-4)}{x^2} or \frac{sin(x)}{cos(x)}$

These functions have derivatives using one rule:

$\frac{(5x-4)}{x^2} -> \frac{5(x^2)-(5x-4)(2x)}{(x^4)}$

Chain rule to calculate a derivative: This may require some memorization, but what is the derivative of (f(g(x))?

$h(x) = (2x-9)^2, then h'(x) = 2(2x-9)*(2)$

Because the function on the inside is 2x-9 and the function on the outside is ( )². The derivative of the outside function is 2( ). Power Rule!! The derivative of the inside function is 2. That means altogether we get 2(2x-9)x2.

Derivatives of sinusodial function: What is the derivative of sin? (If you memorize one, then you know the derivative of cos is similar but has a different sign.)

Integration is Antidifferentiation

Indefinite integral (antidifferentiation): Using the power rule, product rule, and chain rule backwards requires the persistence to check your work over and over again. (Also, remember the last 2 problems we did emphasizing adding in the constant term “+c”)

Bigger Problems

Find the critical points of a function: This is why we take derivatives. The process is to take the derivative and set it equal to 0.

Write the intervals over which the function is increasing or decreasing: Another reason to take the derivative. If the derivative is positive, then the rate of change is positive. If the derivative is negative, then the rate of change is?

Horizontal asymptote of a graph: You can solve these with limits if you are interested in extremely large or extremely negative values. In the middle of a function, you use critical points. Question: Given a function, how will you find the local minimum and local maximum values?

Online Tools

How functions work: https://www.geogebra.org/m/rmqjtbxS
Slope Fields: https://homepages.bluffton.edu/~nesterd/apps/slopefields.html

Topics you memorized for the quiz

Power Rule
Product Rule
Chain Rule
derivative of sin
derivative of cos
derivative of e^x
antiderivative using power rule (If f'(x)=6x, what is f(x)?)

Today let’s go over any of the topics/explanations that you think are troubling. Then, let’s discuss the homework problems that do not seem possible. Note that the calculator is not available but you can quickly sketch graphs by plotting points and calculating critical points.

Word Problems

Scroll through this video to find related rates word problems which use implicit differentiation to solve word problems you will see throughout this semester.