Introduction by Sal
Reading Learning Objectives from OpenStax Algebra & Trigonometry
In this section, you will:
- Plot points using polar coordinates.
- Convert from polar coordinates to rectangular coordinates.
- Convert from rectangular coordinates to polar coordinates.
- Transform equations between polar and rectangular forms.
- Identify and graph polar equations by converting to rectangular equations.
Over 12 kilometers from port, a sailboat encounters rough weather and is blown off course by a 16-knot wind (see Figure 1). How can the sailor indicate his location to the Coast Guard? In this section, we will investigate a method of representing location that is different from a standard coordinate grid.
Figure 1
Plotting Points Using Polar Coordinates
When we think about plotting points in the plane, we usually think of rectangular coordinates(𝑥,𝑦)in the Cartesian coordinate plane. However, there are other ways of writing a coordinate pair and other types of grid systems. In this section, we introduce to polar coordinates, which are points labeled (𝑟, 𝜃) and plotted on a polar grid. The polar grid is represented as a series of concentric circles radiating out from the pole, or the origin of the coordinate plane.
The polar grid is scaled as the unit circle with the positive x-axis now viewed as the polar axis and the origin as the pole. The first coordinate𝑟is the radius or length of the directed line segment from the pole. The angle 𝜃, measured in radians, indicates the direction of 𝑟. We move counterclockwise from the polar axis by an angle of 𝜃,and measure a directed line segment the length of𝑟in the direction of 𝜃. Even though we measure 𝜃 first and then 𝑟, the polar point is written with the r-coordinate first. For example, to plot the point (2, 𝜋/4),we would move 𝜋/4 units in the counterclockwise direction and then a length of 2 from the pole. This point is plotted on the grid in Figure 2.
Example 1
Plotting a Point on the Polar Grid
Plot the point (3, 𝜋/2) on the polar grid.
Solution
The angle𝜋 /2 is found by sweeping in a counterclockwise direction 90° from the polar axis. The point is located at a length of 3 units from the pole in the 𝜋/2 direction, as shown in Figure 3.
Plot the point (2, 𝜋/3)in the polar grid.
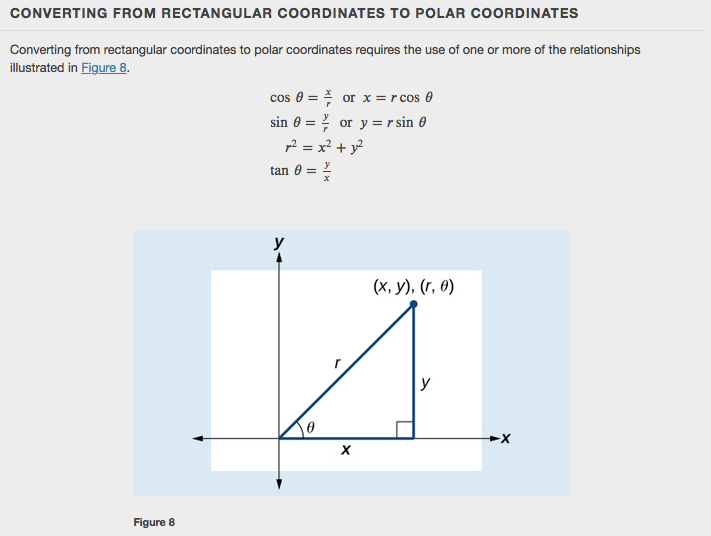
Converting from Rectangular Coordinates to Polar Coordinates
To convert rectangular coordinates to polar coordinates, we will use two other familiar relationships. With this conversion, however, we need to be aware that a set of rectangular coordinates will yield more than one polar point.
Review with Sal
Questions for Practicing
Algebraic
For the following exercises, convert the given polar coordinates to Cartesian coordinates with 𝑟>0 and 0≤𝜃≤2𝜋. Remember to consider the quadrant in which the given point is located when determining 𝜃 for the point.
6. (7, 7𝜋/6)
7. (5, 𝜋)
8. (6, −𝜋/4)
9. (−3, 𝜋/6)
10. (4, 7𝜋/4)
For the following exercises, convert the given Cartesian coordinates to polar coordinates with 𝑟>0, 0≤𝜃<2𝜋. Remember to consider the quadrant in which the given point is located.
11. (4, 2)
12. (−4, 6)
13. (3, −5)
14. (−10,−13)
15. (8, 8)
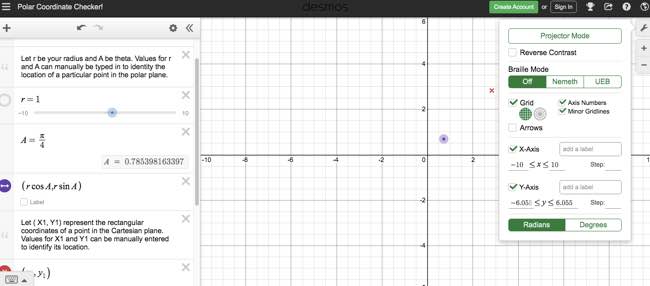
Checking Plot-Pointing Questions. This calculator allows you to plot polar and rectangular coordinates on the same graph. If the points are in the same location, then your answer is correct. (You can also change the calculator from radians to degrees.)
For the following exercises, convert the given Cartesian equation to a polar equation.
16. 𝑥 = 3
17. 𝑦=4
18. 𝑦=4𝑥2
19. 𝑦=2𝑥4
20. 𝑥2+𝑦2=4𝑦
21. 𝑥2+𝑦2=3𝑥
22. 𝑥2−𝑦2=𝑥
23. 𝑥2−𝑦2=3𝑦
24. 𝑥2+𝑦2=9
25. 𝑥2=9𝑦
26. 𝑦2=9𝑥
27. 9𝑥𝑦=1
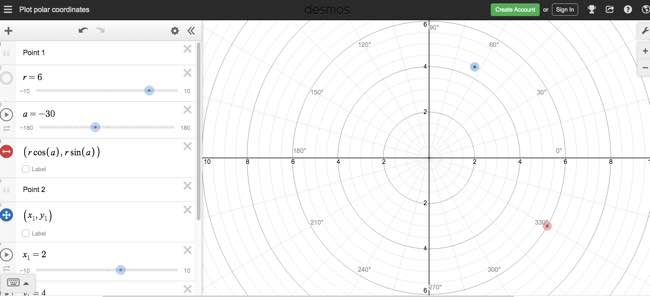
Need Additional Practice? Click on this image of a calculator on Desmos that explores polar coordinates by changing the radius (r) or the angle (a).